这学期终于恢复了常态化学习。本篇笔记大致梳理脉络以及提供学习reference。以后重新整合概率统计、机器学习、最优化、模式识别的内容。还没有完全想好应该怎么记笔记，目前的想法是无纸化写公式，纸上多写写例子（可以拍照传上来，这样就多了一个网站优化图片加载速度的todo）。

考试

题目

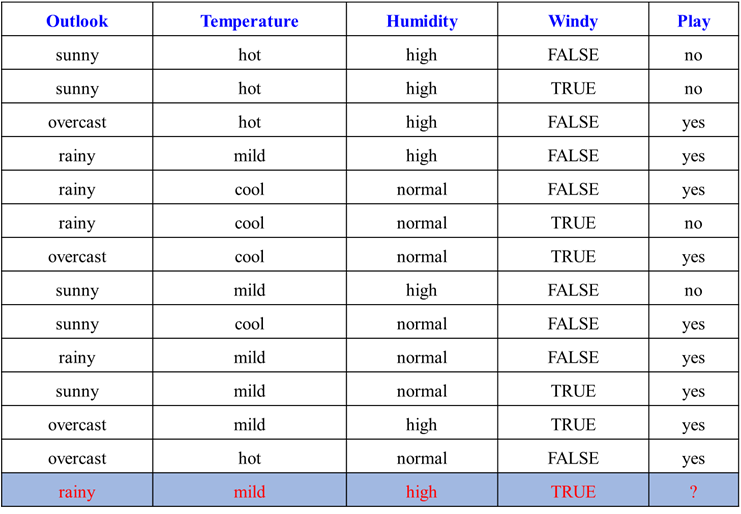
考试要求

针对考试整理一下脉络：

数据预处理：处理噪声、归一化（why&how）、不平衡数据
分类算法：三种分类方法；划分训练集（是否产生影响）；不同性能度量和适配度；参数对结果的影响；算法优缺点
集成学习：把分类问题转化为集成学习问题；一种集成方法；对比集成方法和分类方法
聚类：把分类问题转化为聚类问题；一种聚类方法；参数的影响；算法初始化的影响
异常检测：聚类改成异常检测；求解；
关联规则：两种方法；求解

一般的数据挖掘问题还需要处理缺失值、特征选择（降维）。题目没有缺失值、维度不高所以无所谓。

大致思路

数据预处理

处理噪声

这边不太会处理这道题
(24条消息) 数据挖掘：数据清洗——数据噪声处理_AvenueCyy的博客-CSDN博客_数据噪声处理
这个写的挺好的。（吐槽：我尼玛还在用csdn，以前记的升级平台现在都忘了有啥了，好像有stackoverflow吧。考完看看去）
题目由于主要是标称数据，如果不用相似性分析的话首先需要数值化。不数值化的话感觉没什么噪声。

归一化

归一化参考文章：
数据归一化 - 知乎 (zhihu.com)
理论课上有讲。数值化后需要归一化，把所有数据归一化到均值为0方差为1的分布中。KNN对尺度很敏感，如果不归一做出来天差地别。

简单地除以最大值
最值归一化（Normalization）$$ x_{scale}=\frac{x-x_{mean}}{x_{scale}} $$
均值归一化（Standardization）$$ x_{scale}=\frac{x-x_{min}}{x_{max}-x_{min}} $$

不平衡数据

Collect more data
改变performance metric
采样
生成合成样本
尝试不同算法
惩罚模型，给分错少数类的模型更多惩罚。
变换视角
其他

主要用分层采样。上下采样。

下、欠采样、Undersampling
- Easy Ensemble：多数类随机采样n次，训练n个模型，集成学习
- Balance Cascade：多次欠采样得到Adaboost，对全体多数类预测，控制分类threshold，判断正确就删除该多数类样本。
上、过采样、Oversampling
- SMOTE：对少数类样本$x_i$，计算k近邻，确定采样倍率N，在这N个最近邻$\widehat{x_i}$的连线上随即插值一点作为新的样本，产生因的数据集。
- Borderline-SMOTE：将少数类分为safe、danger和noise。用danger进行SMOTE。
  - safe：k近邻中一半以上为少数类。
  - danger：k近邻中一半以上为多数类。
  - noise：k近邻均为多数类。视为噪声。

分类算法

三种

相似度度量：Jaccard、cosine、Pearson

Jaccard相关性
$$J=\frac{f_{11}}{f_{01}+f_{10}+f_{11}}$$
cosine相关性
$$cos(d_1,d_2)=\frac{⟨d_1,d_2⟩}{\lVert d_1 \rVert\lVert d_2 \rVert}$$
Pearson相关性
$$corr(x,y)=\frac{s_{xy}}{s_xs_y}$$
$$s_{xy}=\frac{1}{n-1}\textstyle\sum_{k=1}^n(x_k-\overline{x})(y_k-\overline{y})$$
$$s_{x}=\sqrt{\smash[b]{\frac{1}{n-1}\textstyle\sum_{k=1}^n(x_k-\overline{x})^2}}$$
$$s_{y}=\sqrt{\smash[b]{\frac{1}{n-1}\textstyle\sum_{k=1}^n(y_k-\overline{y})^2}}$$
决策树：Gini、熵
原则是分得越开越好，Gini和熵越低越好。这里最小化信息熵需要后续参考reference
区别两种划分：
M为度量，Gini或熵。
$$Gain=max{M_0-M_{12},M_0-M_{34}}$$
GINI
- CART基于GINI建立。
Entropy
随机森林：CART(Classification and Regression Trees)
随机森林重要且唯一的参数——决策树的数量m。难以决定的原因在于，m增大任意两树的相关性会增大，错误率上升；但是分类能力增加，错误率降低。
随机森林的重要特征：能够计算单个特征变量的重要性。
- OOB数据(Out-of-bag)：对树k，一些训练实例没有参与其生成，称这些数据为OOB样本。
- 特征重要性
  - 对每棵树用OOB计算其误差errOOB1
  - 对OOB中的特征X加入噪声干扰，计算出errOOB2
  - 对N棵树，特征重要性=$\sum(errOOB2-errOOB1)/N$

Adaboost

找到若干弱分类器，通过计算分类器的权重和点的权重迭代。
迭代过程
- 点的权重$w=\frac{1}{N}$，错误率$\epsilon=\sum_{wrong}w_i$，选出错误率最小的弱分类器，算出其权重$\alpha=\frac{1}{2}\log\frac{1-\epsilon}{\epsilon}$，得到新的集成训练器$f(x_i)=\sum_{t=1}^T\alpha_ih_t(x_i)$，得到所有点的新权重:
  $$w_{new}=\begin{cases}
  \frac{w_{old}}{2(1-\epsilon)}&\text{if classified correctly}\
  \frac{w_{old}}{2\epsilon}&\text{if classified wrongly}
  \end{cases}
  $$

KNN

求k近邻，投票。

Naive Bayes
贝叶斯分类器：
- $$argmax P(Y|X_1,X_2,…X_n)$$$$P(Y|X_1,X_2,…X_n)=\frac{P(X_1,X_2,…X_n|Y)P(Y)}{P(X_1,X_2,…X_n)}$$其中$P(X_1,X_2,…X_n|Y)$为likelihood（自然函数），$P(X_1,X_2,…X_n|Y)$为条件概率，$P(Y)$为prior（先验概率），$P(X_1,X_2,…X_n)$为Nomalization Constant（归一化因子）。
朴素贝叶斯假设：
$$P(X_1,X_2,…X_n|Y)=\prod_{i=1}^nP(X_i|Y)$$
即假设每个条件概率独立。
朴素贝叶斯训练
- Prior$$P(Y=v)=\frac{Count(Y_i=v)}{\text{Count(record)}}$$
- Likelihood$$P(X_i=u|Y=v)=\frac{Count(X_i=u\bigwedge Y_i=v)}{Count(Y=v)}$$
  SVM
核心：间隔、对偶、核技巧
解决问题：
- $$
  \begin{equation} min_{w,b} \frac{\lVert w^2 \rVert}{2}\
  s.t. y_i(w\cdot x_i+b)\ge 1.\
  i=1,2,…n.
  \end{equation}
  $$
凸优化问题：转化为对偶问题。
拉格朗日函数：
$$L(w,b,\alpha)=\frac{\lVert w^2 \rVert}{2}-\sum_{i=1}^N\alpha_i(y_i(wx_i+b)-1)(\alpha_i\ge0)$$
- 需要解决的的问题就是：$min_{w,b}max_{\alpha_i \ge0}L(w,b,\alpha)$
- 化为对偶问题，用KKT条件求解，得到：
  - $\tag{1} \sum_{i=1}^N\alpha_iy_ix_i=w$
  - $\tag{2} \sum_{i=1}^N\alpha_iy_i=0$
  - $\tag{3} -(y_i(wx_i+b)-1)\le 0$
  - $\tag{4} \alpha_i\ge0$
- 只需要再满足$\tag{5} \alpha_i(y_i(wx_i+b)-1)=0$，支持向量需要满足这个条件，其他点$\alpha_i=0$。
  - 故而只需求解：$max_{\alpha_i\ge 0}(\sum \alpha_i-\frac{1}{2}\sum\alpha_i\alpha_jy_iy_jx_i\cdot x_j)$。得出了$\alpha$其他就很明朗了。
核技巧
- 升维使得样本点线性可分。
软硬件隔

划分训练集
hold-out、分层采样、bootstrap、（p次）k折交叉
都是OOB。

不同性能度量和适配度
ACC
AUC：泛化能力强的AUC高。
Recall
混淆矩阵

算法优缺点

决策树：
1. 优点：
  1. 容易理解
  2. 易于生成规则
2. 缺点：
  1. 过于简单
随机森林
1. 优点：
  1. 不需要太多调参
  2. 准确率高
  3. 能运行于大规模数据集
  4. 能处理高维特征数据
  5. 能估计每个特征在分类上的重要性
  6. 对缺省值问题能获得很好的结果
2. 缺点
  1. 在噪声较大的问题上会过拟合
  2. 有不同级别的属性的数据随机森林产出的属性权值可信度低。
  3. 模型过于general
Adaboost
1. 优点
  1. 利用弱分类器进行级联，可以将不同的分类器设置为弱分类器
  2. 具有很高的精度
  3. 充分考虑每个分类器的权重
2. 缺点
  1. 弱分类器数目不好确定
  2. 数据不平衡导致精度下降
  3. 训练耗时
KNN
1. 优点
  1. 简单但可以解决复杂的问题
  2. 训练样本少也可以使用KNN
2. 缺点
  1. 特征选择问题导致结果很多
  2. 对于特征表达过于敏感
朴素贝叶斯
1. 优点
  1. 返回概率，可以得到算法的可信度
  2. 不需要太多训练数据
  3. 很容实现
2. 缺点
SVM
1. 优点
  1. 数学理论基础扎实
  2. 在未知数据上的泛化误差小

集成学习

集成学习（Ensemble Learning) - 知乎 (zhihu.com)

随机森林（Bagging），参考分类模块。考试时在这里回答。
Adaboost（Boosting），参考分类模块。考试时在这里回答。
对比集成学习和分类
集成学习可以整合各个分类器的优点，但也容易过拟合。
聚类
K-means基于距离
similarity，参考分类模块。
DBSCAN基于密度
- $\varepsilon$为半径
- MinPts为领域内至少包含的对象数目
- Border、Core、Outliner
- 直接密度可达、间接密度可达、密度相连
- 优缺点：
  - 簇可以有任意的形状大小
  - 簇的数量自动确定
  - 可以将簇与噪声分开
  - 对噪声鲁棒性较高
  - 参数难以确定
  - 对参数较敏感
    异常检测
    种类
    基于密度（统计）
    $$p(x)=\prod_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma_j^2})\
    \text{Anomaly if }p(x)<\epsilon.
    $$
    $\epsilon$是threshold参数。

将聚类转化为异常检测

基于距离，对象异常值分数为与第k个最近邻的距离。
基于密度，是对象周围密度的倒数。
- 优化为相对密度：
  - $\frac{dist(x,y)}{\sum dist(y_i,k)/k}$
  - $\frac{\sum density(y_k,k)/k}{density(x,k)}$

关联规则

两种方法

Ariori

评价指标：
- Support(S)：同时包含X与Y的Transaction的比例，minsup为阈值
- Confidence(c)：Y出现在含有X的Transaction的比例，minconf为阈值
挖掘关联规则
- 生成频繁项集解决support
- 生成规则解决confidence
  - 连接
  - 修建
    FP tree

Information Retrieval and Web Search

后天考试，明天整理一遍所有内容顺便解一遍题，把文字回答部分讲讲清楚，算法优劣等等。

RoomA

专业学习|数据挖掘

考试

题目

考试要求

大致思路

数据预处理

处理噪声

归一化

不平衡数据

分类算法

三种

相似度度量：Jaccard、cosine、Pearson

决策树：Gini、熵

随机森林：CART(Classification and Regression Trees)

Adaboost

KNN

Naive Bayes

SVM

划分训练集

不同性能度量和适配度

算法优缺点

集成学习

对比集成学习和分类

聚类

异常检测

种类

基于密度（统计）

将聚类转化为异常检测

关联规则

两种方法

Ariori

FP tree

Information Retrieval and Web Search